Defining the measurement surface, GCS & PCS

~~Mapping Surfaces: (Bolstad, Ch. 2, 29 – 39)~~

~~Spatial Referencing Systems (Bolstad, Ch. 3, 85 – 146)~~

Coordinate System Jargon: geoid, datum, projection ( YouTube Video )

Spheroids, Ellipsoid, and Geoid – GIS Fundamentals and Mapping ( YouTube Video )

Recall that:

points are represented by an X&Y coordinate
lines are represented by a series of connected points
polygons are created when an area is enclosed by a line
rasters are a series of square cells (ideal for representing a continuous surface)

2-dimensional locations are defined by an X and Y coordinate pair

3-dimensional locations are defined by an X, Y, and Z coordinate

THIS IS IMPORTANT! How are these X, Y, and Z values referenced to the Earth’s surface? You can NOT assume that all X, Y, and Z values are the same! Some X and Y coordinates measure in feet, some measure in meters, and some measure using degrees. The Z value typically represents elevation, but elevation can be measured in feet, meters, centimeters, and many/any other unit desired.

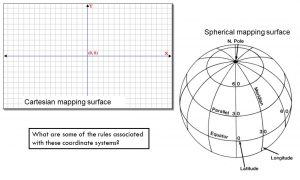
The mapping surface

Before we can map a feature (a thing) in the GIS, we must define the the surface on which they will be mapped. If we don’t do this, nobody will know what or where the coordinate pair, (x:296000, y:3580000) for example, falls on the surface of the Earth. Furthermore, you want to apply the same mapping surface for all features mapped or analyzed in a project. Even more, some mapping surfaces work well in some areas but not others. We will explore approaches to defining the this surface using a Spherical coordinate system and a Cartesian coordinate system.

Spherical coordinate system:

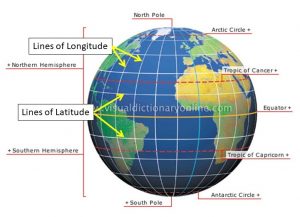
uses two angles of rotation (latitude and longitude) and a radius distance to specify locations
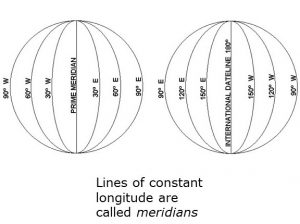
lines of longitude flow through both the north and south pole
- the origin (the line of zero longitude), called the Prime Meridian, flows through the Royal Greenwich Observatory in England
- measures east-to-west and west-to-east
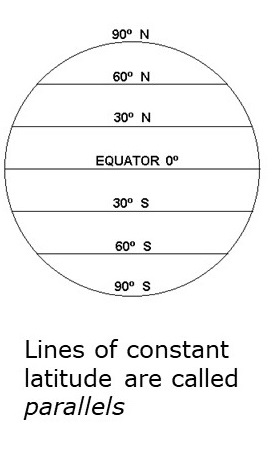
lines of latitude flow perpendicular to the Prime Meridian (and parallel to the equator)
- the origin (the line of zero latitude) is the Equator
- lines of constant latitude are called parallels
radius distance is measured from the center of the earth (https://www.youtube.com/watch?v=MiQWcD25K0w)
spherical coordinate systems, ie. Lat/Long, are NOT a Cartesian coordinate system because lines of longitude converge
they are associated with geographic coordinate systems

Cartesian coordinate system:

a 2-dimensional (XY) or 3-dimensional (XYZ) measuring system defined by orthogonal axes (the lines representing the x-axis and the lines representing the y-axis form right angles)
the origin is defined with zero values
suitable for maps over relatively small areas (sub-state)
associated with projected spatial reference systems like UTM and State Plane

Geographic Coordinate System (spherical mapping surface) (MORE INFORMATION)

A geographic coordinate system (GCS) uses a three-dimensional spherical mapping surface to define a point on the Earth’s surface. Most GPS receivers default to recording locations using latitude, longitude, elevation – this is a GCS.

Components of a GCS

GEOID: a 3D model of the Earth’s bumpy surface
- (oceanservice.noaa.gov) If we were able to remove the effects of the varying tides and currents from the ocean, it would settle onto a smoothly undulating shape (rising where gravity is high and sinking where gravity is low) forming. This irregular surface forms the geoid.
SPHEROID (also might be referred to as the ELLIPSOID): a mathematically-derived surface that approximates the geoid; we need this because the geoid is way too bumpy to measure accurately and it is always changing
- this is the smooth surface on which we overlay our measuring grid
- there is not one spheroid that works best for all areas of the Earth
- spheroids we use in the US:
  - Clarke 1866
  - GRS 1980 (GRS80)
  - WGS 1984 (WGS84)

DATUM: a set of rules uniquely associated with a particular spheroid which defines the origin and orientation of the measuring grid
- defines where, for instance, the Prime Meridian is located, where the standard parallels are and how many are used, and the unit of measure (where we start measuring, the units of measure, how we count, etc)
- datums we use in the US:
  - North American Datum of 1927 (NAD27) – associated with the Clarke 1866 spheroid
  - North American Datum of 1983 (NAD83) – associated with the GRS 80 spheroid
  - World Geodetic System of 1984 (WGS84) – associated with the WGS84 spheroid
- WGS84 is the best fit globally
- NAD83 and NAD27 are better fits for areas in North America
- every GIS layer is referenced to a datum
- you can introduce errors in your maps and analyses if you try to combine layers with different datums
- REMEMBER that each datum uses a different spheroid and each have different sets of measurement rules; if you mis-specify a datum, your data will not be shown in the correct location when you display it in the GIS

GCS Lat/Long

uses degrees of latitude and longitude to describe a location on the Earth’s surface
- datum: WGS84 (can also use NAD27 and NAD83)
- origin
  - East-West (longitude): Royal Greenwich Observatory England
  - North-South (latitude): the equator
- measurement unit is degrees and can be expressed as either ‘decimal degrees’ or ‘degrees/minutes/seconds’
latitude: horizontal lines running parallel to the equator (think of the steps on a ladder)
- values range from -90 to 90
  - South Pole = -90 degrees
  - Equator = 0 degrees
  - North Pole = 90 degrees
- parallels measure north-south distance from equator, the Y-value
- Anywhere on the Earth’s surface, one degree of latitude equals 60 nautical miles
longitude: vertical lines running perpendicular to the equator and through the north and south pole
- values range from -180 to 180
  - Greenwich, England = 0 degrees
  - Values are negative west of 0 (this is us)
  - Values are positive east of 0
  - measures east-west distance from the Prime Meridian, the X-value
  - one degree of latitude equals 60 nautical miles only at the equator
    - meridians converge as one heads to either pole
      - 1 degree of longitude (east-west distance) at the equator is larger than 1 degree of longitude near the poles
  - Since degrees of longitude are not constant for all the Earth’s surface, geographic spatial reference systems should not be used when area or distance calculations are required

Convert degrees/minutes/seconds (DMS) to decimal degrees (DD)

Know that there are:
- 60 minutes in 1 degree
- 3600 seconds in 1 degree
DMS to DD
- Latitude: D + (M/60) + (S/3600)
- Longitude: (D + (M/60) + (S/3600)) * -1
  - multiply by -1 since we are in the western hemisphere
Warnell campus (in DMS): 33°56’39″N, 83°22’32″W
- (39/3600) + (56/60) + 33 = 33.9335
- [(32/3600) + (22/60) + 83] * -1 = -83.3668

Projected Coordinate System (2D or 3D mapping surface)

Spherical coordinate system works well for mapping locations on a round surface. However, if you need to produce a flat map, you must figure out a way to accurately flatten that round surface. We use a map projection for this task. Be careful, though, this process WILL introduce error (in shape, size, direction). Your task is to select a map projection that minimizes these errors.

“Map Projection” A method by which the curved surface of the Earth of portrayed on a flat surface. This generally requires a systematic mathematical transformation of the lines of longitude and latitude onto a plane. (from the ArcGIS 9.2 Desktop online help)

Projections are designed to minimize distortion in one or more of the following areas:

Area (equivalent or equal area)
Distance (equidistant)
Direction (azimuthal)
Shape (conformal)

Two map projections you need to be familiar with: Lambert Conformal Conic and Transverse Mercator

Both are conformal projections
Conformal projections attempt to minimize distortation of shape
Distances are true only along the standard parallel or central meridian
- recall that parallels run parallel to the Equator and meridians run perpendicular to the Equator
Distortion of distance, area, and direction increase with distance from the central meridian or standard parallels

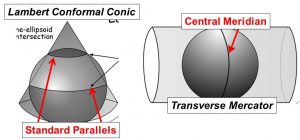
Distances are true only along the central meridian or standard parallels
Distortion of distance, area, and direction increase with distance from the Cntral Meridian and standard parallel(s)

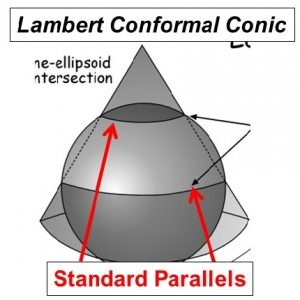
Lambert Conformal Conic

The user specifies where the standard parallels (lines of latitude) are located – they can be as close or far apart as desired
- A user interested in mapping an east-west oriented state like Tennessee 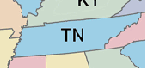might select standard parallels that cross the northern half and the southern half of the state. In this case, distortion of the areas that fall under these standard parallels would be minimized.

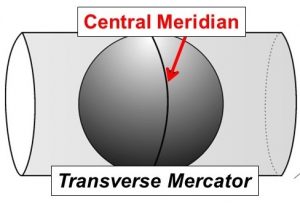
Transverse Mercator

The user specifies where the central meridian (lines of longitude) are located
A user who is interested in mapping a north-south oriented state like Alabama 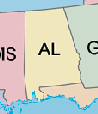might choose a central meridian that runs through the center of the state
- In this case, distortion would be the least in the middle of the state and would gradually get larger as one moves to the edges.

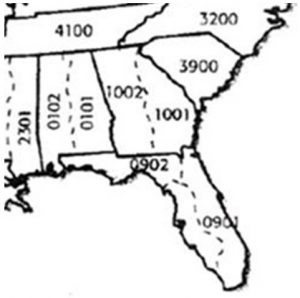
The state plane coordinate system:

Each US state has at least one state plane zone
- Some states have multiple zones (Georgia has ‘east’ and ‘west’ State Plane zones)
Uses either the Transverse Mercator (north-south oriented states) or Lambert Conformal Conic (east-west oriented states)
- Georgia State Plane uses the Transverse Mercator map projection
- Tennessee State Plane uses the Lambert Conformal Conic map projection
Uses feet as its native unit of measurement
Traditionally used the North American Datum of 1927 (NAD27)
Not sure which SP zone you are in?
- USA State Plane Zones

The Universal Transverse Mercator (UTM) coordinate system

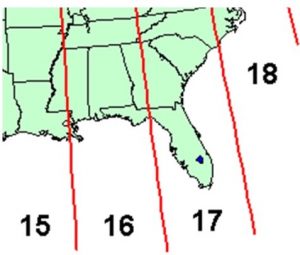
Earth split into 60, 6-degree zones
- eastern Georgia is in UTM zone 17
- western Georgia is in UTM zone 16
Measurements are made in meters
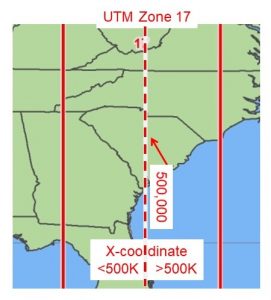
The X coordinate of the center of every UTM zone, the central meridian, is arbitrarily set to 500,000m
- as you move eastward, the X-value increases
- as you move westward, the X-value decreases
The Y coordinate is the distance from the equator, measured in meters
Utilizes the NAD 1983 datum
Not sure what UTM zone you are in?
- What UTM zone am I in?

In practice

Select a coordinate system with the least distortion for your project area
Look to see what coordinate system the ‘experts’ use
For most small area projects, the State Plane or UTM coordinate systems are equally good
If project overlaps state boundaries, UTM is often a better choice
Important to make sure all data and all people (on a given project) are using the same coordinate system